Inhaltsverzeichnis
Kompetenzmodelle zum Zahlverständnis
Zitiervorschlag: Rauner, R., Stecher, M. (2021). „Kompetenzmodelle zum Zahlverständnis.“ Abgerufen von URL:https://wsd-bw.de/doku.php?id=wsd:mathematik:zahlverstaendnis, CC BY-SA 4.0
Entwicklungsmodell zum Zahlverständnis nach Fritz und Ricken, ergänzt durch Fuson
Es ist davon auszugehen, dass Kinder bereits vor der ersten hier beschriebenen Kompetenzebene über frühe mathematische Konzepte (Vergleichen, Vermehren, Vermindern) verfügen, ohne diese mathematisch präzise anwenden zu können.
Die Entwicklung des Zahlverständnisses kann in Anlehnung an Fritz und Ricken et al (vgl. Fritz, Ricken et al 2007) sowie unter Berücksichtigung des theoretischen Konzepts nach Fuson, welches den Übergang vom ordinalen zum kardinalen Zahlverständnis konkretisiert (vgl. Fuson 1998), über vier Kompetenzebenen beschrieben werden.
Kompetenzebenen Zahlverständnis
| Kompetenzebene I: Ordinales Zahlverständnis | |
|---|---|
| 1. Basales Verständnis für Mengeneigenschaften: Bereits auf dieser Kompetenzebene gelingt es Kindern, Gegenstände nach ihren Eigenschaften zu ordnen und zu vergleichen. In Alltagszusammenhängen können Mengen aus unterschiedlichen Elementen gebildet werden. Beispiel: Bauklötze ihrer Länge nach in eine Reihenfolge bringen. | |
| 2. Ganzheitsauffassung der Zahlwortreihe: Das Aufsagen der Zahlwortreihe ist hier noch nicht als Zählstrategie zu verstehen, vielmehr wird diese hier als unidirektionale Ganzheit erfasst und daher wie ein Gedicht aufgesagt. Ein Abzählen oder eine Eins-zu-Eins-Zuordnung von Zahl und Objekt ist damit noch nicht möglich. Beispiel: einszweidreivierfünf… | |
| 3. Unflexible Zahlwortreihe: Die Unterscheidung der einzelnen Zahlwörter gelingt. Zahlen werden für Zählhandlungen eingesetzt. Beim Abzählen wird in der Zahlwortreihe allerdings immer bei 1 begonnen, eine beliebige Zahl kann noch nicht als Ausgangspunkt genutzt werden. Beispiel: Eins-zwei-drei-vier-fünf… | |
 Übergang vom ordinalen zum kardinalen Zahlverständnis | 4. Teilweise flexible Zahlwortreihe: Hier setzt bereits der Übergang vom ordinalen zum kardinalen Zahlverständnis ein. Es gelingt, beim Zählen irgendwo in der Reihe zu beginnen. Auch der Vorgänger und Nachfolger einer Zahl können bereits sicherbenannt werden. Beispiel: sieben-acht-neun-zehn → zehn-neun-acht… |
| 5. Flexible Zahlwortreihe: Von jeder Zahl aus kann nun um eine bestimmte Anzahl weitergezählt werden. Auch erste Additionsstrategien werden eingesetzt. Beispiel: fünf… sechs-sieben-acht… neun… zehn-elf-zwölf… dreizehn | |
| 6. Vollständig reversible Zahlwortreihe: Abschnitte der Zahlwortreihe können nun vor- und rückwärts gezählt werden, dabei gelingen auch Richtungswechsel ohne Schwierigkeiten. Zu den Additionsstrategien kommen Strategien zur Subtraktion hinzu. Beispiel: 8-5=3 → 3+5=8 | |
| Kompetenzebene II: Kardinales Zahlverständnis | |
| Kinder vertiefen auf dieser Ebene ihr Wissen über die Zahlwortreihe. Das Zählen von Abschnitten der Zahlwortreihe in beide Richtungen gelingt nun sicher, genauso die Nutzung von Additions- und Subtraktionsstrategien. Visuell gestützt ist die Ergänzung von einer Teilmenge zu einer Gesamtmenge möglich. | |
| Kompetenzebene III: Teil-Teil-Ganzes-Verständnis | |
| Auf dieser Kompetenzebene gelingt es, Teilmengen aus einer Gesamtmenge zu bilden und Unterschiede von Mächtigkeiten zu erfassen (größer als/kleiner als). Außerdem werden Zahlenmuster erkannt und können weitergeführt werden (z.B.: 1-3-5-7…). | |
| Kompetenzebene IV: Relationalität | |
| Auf dieser Ebene gelingt die Bestimmung der Differenz zwischen zwei Mengen (z.B. „Wie viele sind es mehr/weniger?“, „Nenne die Zahl, die um 2 größer ist als 7!“). Auch das Rückwärtszählen in Schritten gelingt. | |
Nutzung von Zählstrategien - Modell der Overlapping Waves nach Siegler
Beim Erwerb von Zählstrategien lässt sich beobachten, dass diese zunehmend komplexer und effizienter werden. Eine neue Strategie wird dann häufiger verwendet, wenn sie zum Erfolg führt. Weniger entwickelte, einfachere Strategien verschwinden aber nicht. Sie werden immer noch in neuen oder komplexen Situationen angewendet (z. B. bei der Erweiterung des Zahlenraumes), oder wenn es einfach der beste Weg ist, ein Problem zu lösen. Siegler beschreibt dieses Phänomen als overlapping waves (Fritz et al 2017). Aufgrund dieses Phänomens muss die:der Diagnostiker:in in der Arbeitshilfe dokumentieren, in welcher Situation bzw. in welchem Zahlenraum welche Strategie genutzt wird.
Overlapping Waves
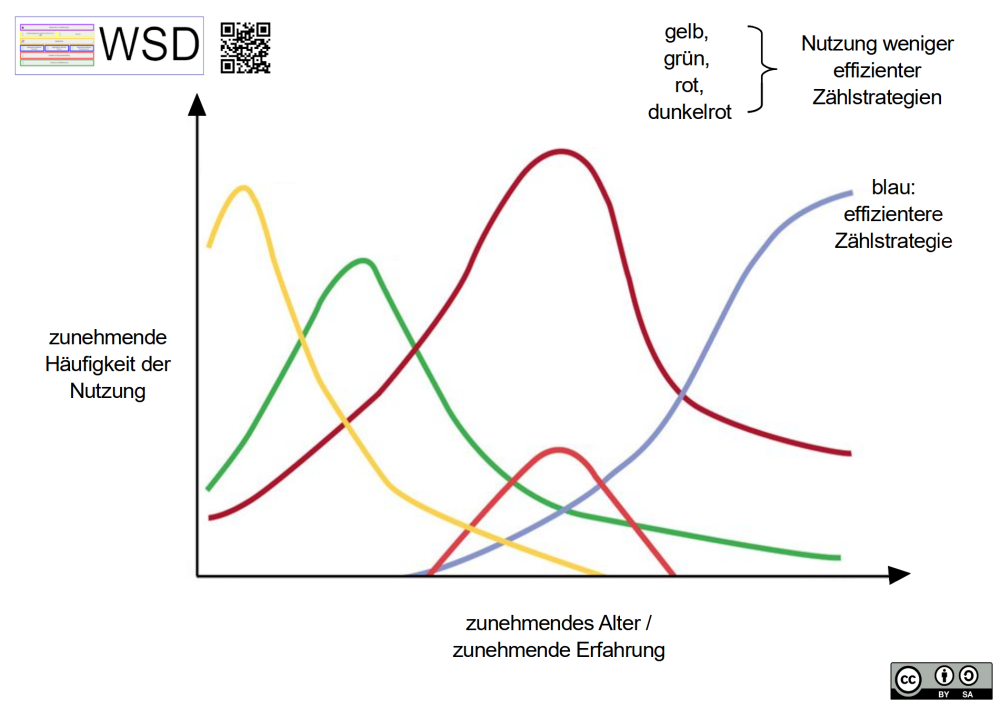
Zitiervorschlag: Grafik „Overlapping Waves“ von Albrecht, C. (2021) nach Siegler, R. (2015). Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:mathematik:zahlverstaendnis#overlapping_waves, CC BY-SA 4.0
Da weder bei einem basalen Verständnis für Mengeneigenschaften noch bei einer Ganzheitsauffassung der Zahlwortreihe Zahlen für Zählhandlungen eingesetzt werden können, wird das Operationsverständnis erst ab der Nutzung einer unflexiblen Zahlwortreihe diagnostisch relevant.
Zusätzlich zum Zahl- und Operationsverständnis muss das Stellenwertverständnis bei einem Zahlenraum größer 20 diagnostisch in den Blick genommen werden.
Weiterführende Informationen
Literatur
Fritz, A.; Ricken, G. & Gerlach, M. (2007). Handreichung zur Durchführung der Diagnose Kalkulie. Diagnose- und Trainingsprogramm für rechenschwache Kinder. Berlin: Cornelsen-Verlag
Fritz, A; Schmidt S. & Ricken, G. (2017). Handbuch Rechenschwäche. Lernwege, Schwierigkeiten und Hilfen bei Dyskalkulie. Weinheim: Beltz Verlag
Fuson, K. (1988). Children’s counting and concept of number. Hamburg: Springer-Verlag
Ricken G., Fritz-Stratmann A, & Balzer L. (2013): Marko-D. Mathematik- und Rechenkonzepte im Vorschulalter-Diagnose. Göttingen: Hogrefe-Verlag
Siegler, R. (2015). How children develop. Duffield: Worth
Schneider W., Küspert P. & Krajewski K. (2016). Die Entwicklung mathematischer Kompetenzen. Paderborn: Schöningh-Verlag
Werner, B. (2009). Dyskalkulie – Rechenschwierigkeiten. Diagnose und Förderung rechenschwacher Kinder an Grund- und Sonderschulen. Stuttgart: Kohlhammer
Layout und Gestaltung: Christian Albrecht, Zentrum für Schulqualität und Lehrerbildung (ZSL) Baden-Württemberg