Kompetenzmodell zum Operationsverständnis

Zitiervorschlag: Rauner, R., Stecher, M. (2021). „Kompetenzmodell zum Operationsverständnis.“ Abgerufen von URL:https://wsd-bw.de/doku.php?id=wsd:mathematik:operationsverstaendnis, CC BY-SA 4.0

In Anlehnung an Schulz et al (2017) wird das Operationsverständnis im Folgenden als die Fähigkeit von Schüler:innen verstanden, Situationen (d. h. Beschreibungen, Handlungen, Bilder, Texte) in passende Rechenoperationen zu übersetzen und umgekehrt zu Operationen passende Situationen zu finden. Zu einem entwickelten Operationsverständnis gehören folglich sämtliche Übersetzungen zwischen den verschiedenen Repräsentationsebenen, wie die folgende Abbildung veranschaulicht (Kaufmann/Wessolowski 2011).

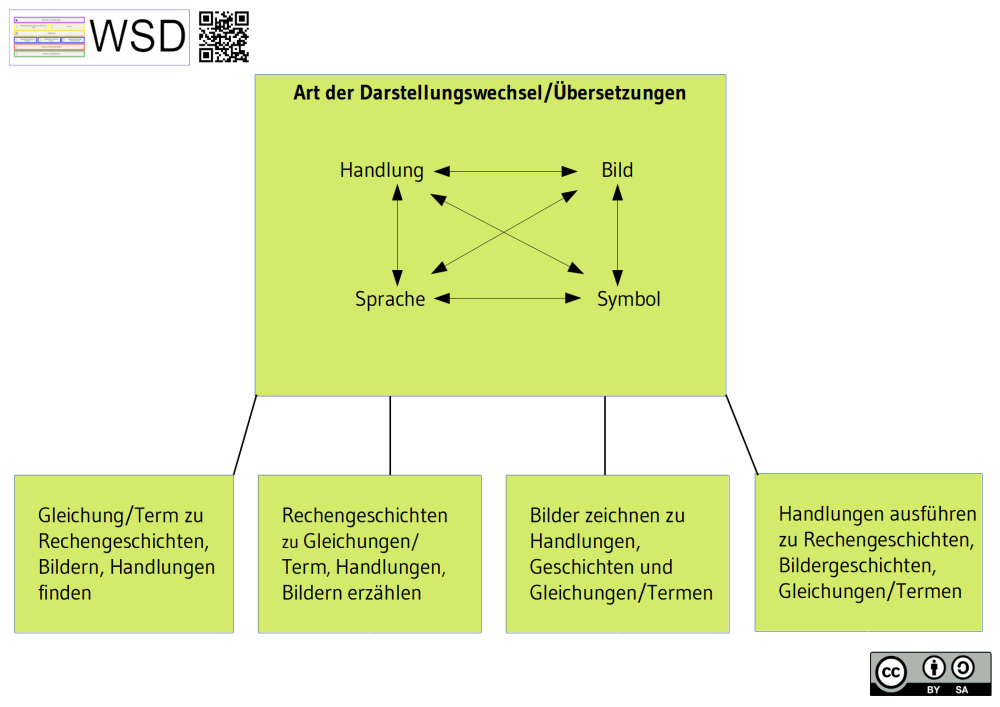
Zitiervorschlag: Grafik „Darstellungswechsel“ von Albrecht, C. (2021) nach Kaufmann, S. & Wesselowski, S. (2011). Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:mathematik:operationsverstaendnis#darstellungswechsel, CC BY-SA 4.0

Auf dieser Basis können in Bezug auf das Operationsverständnis vier Kompetenzebenen (vgl. Schulz et al 2015) beschrieben werden. Auf jeder Kompetenzebene ist eine Beschreibung der bereits gelingenden bzw. noch nicht gelingenden Übersetzungen zwischen den unterschiedlichen Repräsentationsebenen erforderlich.

Eine konkret erfassbare Realsituation kann in eine einschrittige Rechenoperation übersetzt werden, wenn:

• passende Signalwörter gegeben werden,
• die Situation unmittelbar verständlich ist und nicht erst strukturiert werden muss,
• die Werte in der Rechenreihenfolge angegeben sind.

Auf dieser Kompetenzebene werden einfachste Grundvorstellungen zur Addition (z.B. Zusammenfügen), zur Subtraktion (z.B. Wegnehmen) und zur Multiplikation (z.B. räumlich wiederholte Anordnung) benötigt. Grundvorstellungen im Bereich der Division können auf dieser Kompetenzebene noch nicht hinreichend sicher genutzt werden.

Beispiel: Luca hat 8 Bonbons. Er gibt 3 davon ab. Wie viele Bonbons hat er dann noch?

Eine einfache Problemstellung kann auch dann in eine einschrittige Rechenoperation übersetzt werden, wenn:

• abstrakte Beziehungen zwischen den Größen oder Zahlen bestehen,
• die Notwendigkeit einer einfachen gedanklichen Strukturierung der dargestellten Situation notwendig ist,
• die Reihenfolge der genannten Werte oder Signalwörter nicht mehr als Hinweis auf passende Operationen genutzt werden kann.

Auf dieser Kompetenzebene werden Grundvorstellungen zu den vier Rechenarten benötigt.

Beispiel: Sara faltet Papiersterne. Ein Bogen reicht für 3 Sterne. Wie viele Bögen braucht sie für 15 Sterne?

Ein mehrschrittiger Lösungsweg kann auch dann gefunden werden, wenn:

• die dargestellte Situation gedanklich strukturiert und vereinfacht werden muss,
• die Zahlen oder Größen zunächst miteinander in Beziehung gesetzt werden müssen,
• relevante von irrelevanter Information getrennt werden muss,
• Signalwörter und die Reihenfolge der vorgegebenen Werte keine Hinweise auf die passende Operation bieten.

Auf dieser Kompetenzebene muss eine Verknüpfung mehrerer Grundvorstellungen miteinander erfolgen.

Beispiel: Timo will mit Bauklötzen 10 gleiche 8-er-Türme bauen. In seiner Kiste sind 62 Bauklötze. Wie viele Bauklötze fehlen ihm noch? Schreibe deine Rechnung auf.

Eine Situation kann auch dann in eine mehrschrittige Rechenoperation übersetzt werden, wenn:

• die Situation eine ausgeprägte Komplexität und Problemhaltigkeit aufweist,
• sich die Verkettung der einzelnen Rechenschritte erst über die gedankliche Konstruktion der Situation ergibt und nicht durch ein schrittweises Vorgehen gelöst werden kann,
• ein passender Lösungsweg erst konstruiert werden muss, da die mathematische Struktur der Situation nicht vertraut ist.

Auf dieser Kompetenzebene müssen zu den vier Grundrechenarten unterschiedliche Grundvorstellungen aktiviert und miteinander verknüpft werden.

Beispiel: Lena und Sonja haben zusammen 40 CDs. Sonja hat 6 CDs mehr als Lena. Wie viele CDs hat Lena? Schreibe deine Rechnung auf.

Faledia: Lernplattform zur Steigerung der Diagnosekompetenz in Mathematik

Kaufmann, S.; Wessolowski, S. (2011). Rechenstörungen. Diagnose und Förderbausteine. Seelze: Klett Kallmeyer

Schulz, A., Leuders, T. & Rangel, U. (2017). Arithmetische Basiskompetenzen am Übergang zu Klasse 5 – eine empirie- und modellgestützte Diagnostik als Grundlage für spezifische Förderentscheidungen. In Fritz, A./Schmidt, S./Ricken, G. (Hrsg.): Handbuch Rechenschwäche. Weinheim: Beltz

Schulz, A., Leuders, T., Rangel,U. & Kowalk, S. (2015). Lernstand 5 in Baden-Württemberg: Diagnose und Förderung arithmetischer Basiskompetenzen. In: Mathematik lehren 192/2015.

Layout und Gestaltung: Christian Albrecht, Zentrum für Schulqualität und Lehrerbildung (ZSL) Baden-Württemberg