Inhaltsverzeichnis
Kompetenzstrukturmodell für das Fach Mathematik
Zitiervorschlag: Stecher, M. & Rauner, R. (2021). „Kompetenzstrukturmodell für das Fach Mathematik.“ Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:mathematik:kompetenzbereiche, CC BY-SA 4.0
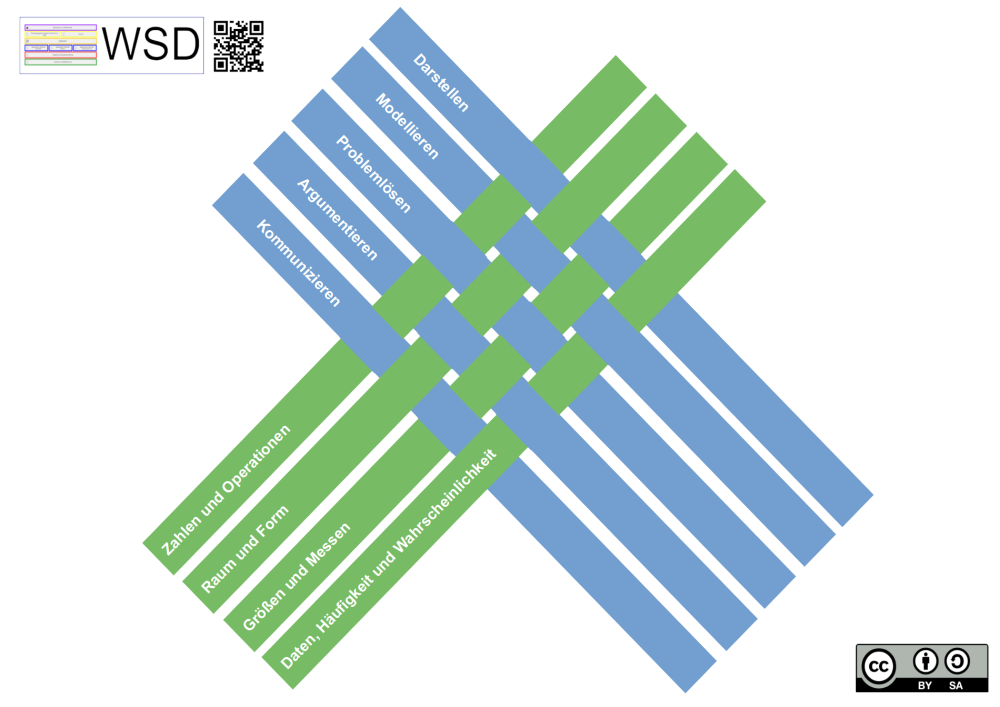
Das im Folgenden dargestellte Kompetenzstrukturmodell ist Grundlage für das Fach Mathematik im Bildungsplan 2016. Das Modell gliedert sich in inhalts- und prozessbezogene mathematische Kompetenzen, die sich in ihrer Vernetzung wie folgt grafisch darstellen lassen (inhaltsbezogene Kompetenzen grün, prozessbezogene Kompetenzen blau):
Vernetzung mathematischer Kompetenzen
Zitiervorschlag: Grafik „Vernetzung mathematischer Kompetenzen“ von Albrecht, C., Stecher, M. & Rauner, R. (2021). Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:mathematik:kompetenzbereiche#vernetzung_mathematischer_kompetenzen, CC BY-SA 4.0
Inhaltsbezogene Kompetenzen
Unter inhaltsbezogenen Kompetenzen sind Kenntnisse und Fertigkeiten, wie z.B. die Beherrschung des Verfahrens der schriftlichen Addition, das Messen von Streckenlängen oder das Bauen von Würfelgebäuden zu verstehen. Im Bildungsplan von 2016 wird zwischen folgenden inhaltsbezogenen Kompetenzbereichen unterschieden:
- Zahlen und Operationen
- Größen und Messen
- Raum und Form
- Daten, Häufigkeit und Wahrscheinlichkeit
Der Bereich Daten, Häufigkeit und Wahrscheinlichkeit wird in der WSD nicht in den Blick genommen.
Prozessbezogene Kompetenzen
Neben den inhaltsbezogenen Kompetenzen ist der Erwerb von prozessbezogenen Kompetenzen (Kommunizieren, Argumentieren, Problemlösen, Modellieren, Darstellen) von besonderer Bedeutung, da diese entscheidend zu einer verständnisorientierten mathematischen Grundbildung beitragen und für eine erfolgreiche Nutzung und Aneignung von Mathematik von zentraler Bedeutung (KMK 2005) sind. Prozessbezogene Kompetenzen beziehen sich auf den Prozess der aktiven Auseinandersetzung mit Mathematik und regen dadurch zur Reflexion von Lösungswegen an.
In der folgenden Tabelle werden die prozessbezogenen Kompetenzen dargestellt, die für den Mathematikunterricht von zentraler Bedeutung sind:
| Kompetenz | Prozess |
|---|---|
| Problemlösen | - Mathematische Problemstellungen bearbeiten - Zusammenhänge durch systematisches Probieren, Reflektieren und Prüfen erschließen - Erkenntnisse übertragen und variieren |
| Modellieren | - Sachsituationen in der Erfahrungswelt erfassen - Diese in mathematische Modelle übertragen und mit Hilfe mathematischer Kenntnisse und Fertigkeiten bearbeiten - Die Lösung auf die Sachsituation zurückbeziehen |
| Argumentieren | - Vermutungen über mathematische Zusammenhänge begründen - Beziehungen und Gesetzmäßigkeiten (sprachlich, handelnd, zeichnerisch) erklären |
| Darstellen/Kommunizieren | - Eigene Denkprozesse oder Vorgehensweisen angemessen und nachvollziehbar darstellen - Austausch mit anderen (in Umgangssprache, zunehmend auch in fachgebundener Sprache) - Nutzung von Darstellungsformen (Skizzen, Tabellen usw.) |
Beispielaufgaben zur integrierten Förderung inhalts- und prozessbezogener Kompetenzen finden Sie unter Hinweise zur Didaktisierung - Mathematik.
Weiterführende Informationen
Literatur
KMK (2005). Bildungsstandards im Fach Mathematik für den Primarbereich. München, Neuwied: Wolters-Kluwer, Luchterhand Verlag
Ministerium für Kultus, Jugend und Sport Baden-Württemberg (2016). Bildungsplan der Grundschule – Mathematik
Selter, C. & Zannetin, E. (2019). Mathematik unterrichten in der Grundschule. Seelze: Kallmeyer
Layout und Gestaltung: Christian Albrecht, Zentrum für Schulqualität und Lehrerbildung (ZSL) Baden-Württemberg