Nicht-zählende Rechenstrategien erarbeiten

Zitiervorschlag: Rauner, R. (2021). „Nicht-zählende Rechenstrategien erarbeiten“. Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:didaktisierung:nicht-zaehlende_strategie, CC BY-SA 4.0

Die ersten Strategien, die Kinder bei der Addition und Subtraktion nutzen, sind Abzählstrategien (Häsel-Weide et al 2017). Wenn im Rahmen des Anfangsunterrichts im Zahlenraum bis 10 gerechnet wird, werden Zählstrategien häufig als sehr erfolgreiche Strategien wahrgenommen, da sie in diesem kleineren Zahlenraum schnell korrekte Ergebnisse liefern (Häsel-Weide et al 2017).

Bei der Entwicklung der Zählstrategien lassen sich vier unterschiedliche Formen beobachten, welche im Sinne eines Entwicklungsprozesses (Phasen der Ausdifferenzierung des Zählens) gesehen werden können, der von Kindern in der folgenden Richtung (allerdings nicht linear und vollständig, sondern teilweise abhängig von der jeweiligen Aufgabe) durchlaufen wird (Häsel-Weide et al 2017):

• Alleszählen: Die Kinder greifen auf die Zahlwortreihe zurück, bei der Addition werden die beiden Summanden beginnend bei 1 ausgezählt und beispielsweise Plättchen werden gelegt. Dann erst werden die Mengen durchgezählt. Häufig werden dabei auch die Finger noch mit genutzt (z.B. 4+3: 1, 2, 3, 4; 1, 2, 3; dabei Plättchen legen; dann erst Gesamtmenge auszählen).
• Weiterzählen vom ersten Summanden aus: Eine Aufgabe wird nicht mehr von 1 aus gezählt, sondern der erste Summand zählt als Startpunkt zum Weiterzählen. Beim Weiterzählen vom ersten Summanden aus ohne Darstellungsmittel kommt es häufig zu Minuseins- oder Pluseins-Fehlern, da das Kind zwei Zahlreihen im Kopf koordinieren muss, um zu erkennen, wann das Ende des zweiten Summanden erreicht ist. Bei der Subtraktion wird diese Koordination besonders schwierig, da die beiden Zahlenreihen gegenläufig sind (Kinder zählen rückwärts und gleichzeitig die Anzahl der Rückwärtsschritte vorwärts mit, z. B. 14-3: 14; 1 Schritt, 13; 2 Schritte 12; 3 Schritte 11).
• Weiterzählen vom größeren Summanden aus: Bei dieser Strategie zählen Kinder immer vom größeren Summanden aus weiter, d. h. sie nehmen die Summanden als solche wahr und beachten deren Größenrelation (4+5=5+4).
• Weiterzählen vom größeren Summanden aus in größeren Schritten: Es wird nun vom ersten Summanden aus in größeren (meist gleichgroßen) Schritten weitergezählt (z. B. 2+6: 2, 4, 6, 8). Im erweiterten Zahlenraum ist auch ein Weiterzählen mit Bezug zum Dezimalsystem möglich (z. B. 15+25: 25, 30, 35, 40).

Verfestigen sich Zählstrategien aber, so kann dies zu Schwierigkeiten in Mathematik führen (Häsel-Weide et al 2017):

• Kinder, die Zählstrategien nutzen, operieren meist ist Einerschritten. Anzahlen werden so nicht strukturiert erfasst und Zahlen werden nicht zu größeren Einheiten zusammengefasst. Auch eine Zehnerbündelung gelingt häufig nicht. Somit wird auch die Einsicht in die dezimalen Strukturen unseres Zahlsystems erschwert.
• Zahlen werden häufig ordinal als ein Punkt in einer Reihe verstanden, als eine Stelle in einer auswendig gelernten Zahlenfolge. Dieses Zahlverständnis erschwert die Ausbildung operativer Strategien.
• Rechenaufgaben werden isoliert voneinander und nacheinander gelöst, ohne auf Beziehungen zwischen einzelnen Aufgaben zu achten, um so Muster und Strukturen erkennen zu können.

Untersuchungen zeigen, dass das verfestigte zählende Rechnen ein charakteristisches Merkmal von Kindern mit Schwierigkeiten im Rechnen ist, das sich auch noch in höheren Schuljahren zeigt (vgl. Geary 2004; Moser Opitz 2007a in Häsel-Weide et al 2017).

Die Ursachen für eine Verfestigung des zählenden Rechnens sind vielfältig und müssen im Rahmen der Hypothesenbildung genauer in den Blick genommen werden: Untersuchungen haben ergeben, dass Kinder mit Schwierigkeiten im Arbeitsgedächtnis (vgl. Grube 2006; Thomas et al. 2006; Krajewski 2008 in Häsel-Weide et al 2017) Probleme bei der Automatisierung des Einspluseins und des Einmaleins haben und daher auf Abzählstrategien zurückgreifen. Aber auch Faktoren der Lernumgebung (wie z.B. eine fehlender Verwendung von Ableitungsstrategien, bei der Addition ein Weiterzählen vom größten Summanden aus) können Zählstrategien begünstigen.

Kinder lediglich dazu aufzufordern, sich vom zählenden Rechnen zu lösen oder beim Rechnen nicht ihre Finger zu benutzen, genügt nicht, da die Entwicklung vom Zählen hin zum Lösen einer Aufgabe mit Hilfe alternativer Strategien ein komplexer Prozess ist. Daher ist es überaus wichtig, bei Schüler:innen beispielsweise über eine kommunikativ-kooperative Strukturierung des Unterrichts Ablöseprozesse anzustoßen, so dass grundlegende Vorstellungen von und Einsichten über Zahlen und Operationen (weiter-)entwickelt werden können (vgl. Häsel-Weide et al).

Häsel-Weide et al (2017) machen konkrete Vorschläge in Bezug auf das Initiieren von Ablöseprozessen:

Kinder sollen Zahlen in Relationen zueinander deuten lernen (Grundlage für das Verständnis von Nachbarschaftsbeziehungen und Teil-Ganzes-Beziehungen)

Beziehung des Ganzen und seinen Teilen verstehen als Grundlage für den Erwerb flexibler Rechenstrategien und damit als Meilenstein in der Entwicklung der mathematischen Kompetenzen. Beispielaufgaben (aus: Häsel-Weide et al 2017):

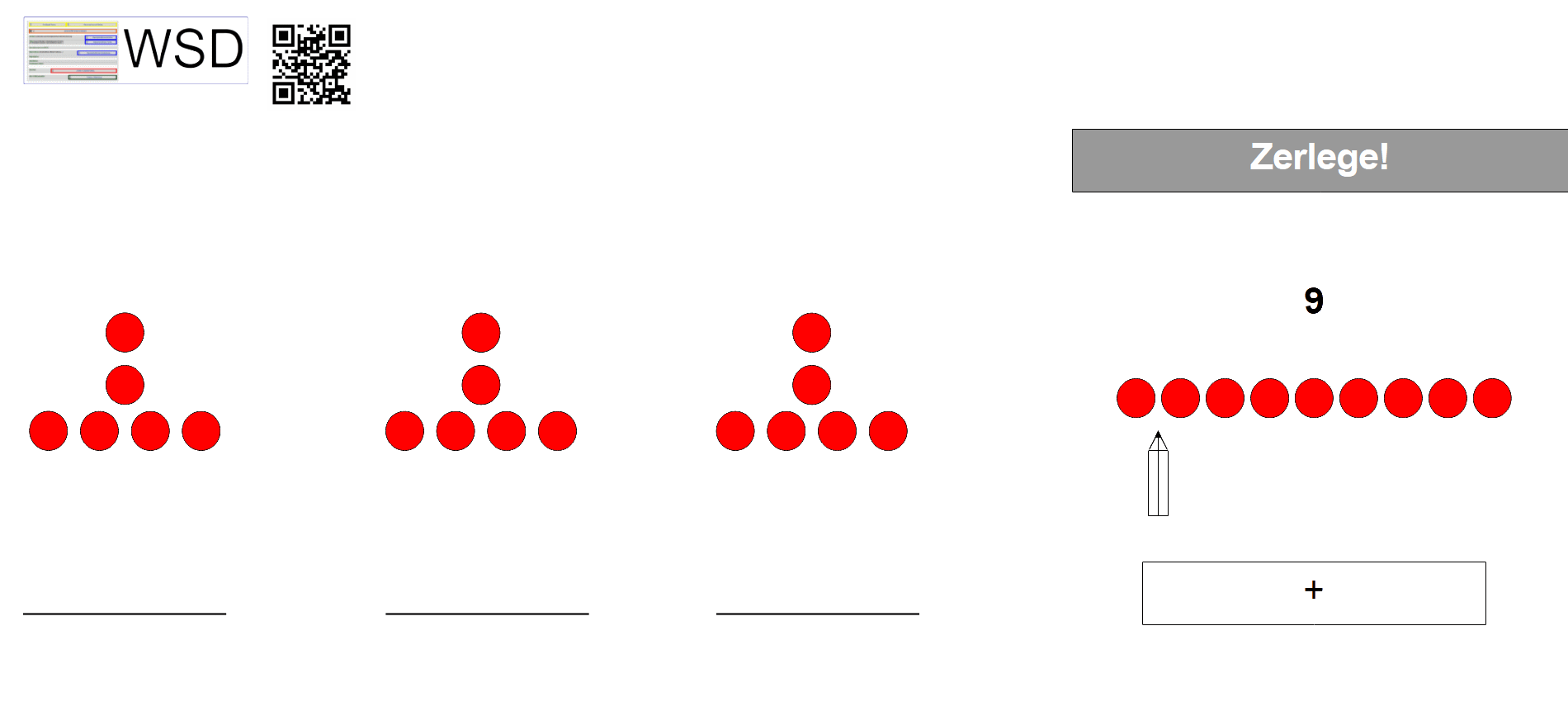
Zitiervorschlag: Grafik „Teil-Ganzes-Zerlegungen erfahren“ von Albrecht, C. (2022). Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:didaktisierung:nicht-zaehlende_strategie#teil-ganzes-zerlegungen_erfahren, CC BY-SA 4.0

Erwerb einer sicheren und flexiblen Zählkompetenz (auch Zählen in größeren Schritten) als Grundlage für die Ablösung vom zählenden Rechnen. Beispielaufgaben (aus: Häsel-Weide et al 2017):

Zitiervorschlag: Grafik „Zählkompetenzen erweitern“ von Albrecht, C. (2022). Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:didaktisierung:nicht-zaehlende_strategie#zählkompetenzen_erweitern, CC BY-SA 4.0

Kinder sollen Mengen vergleichen und verändern, um eine Grundvorstellung von Addition und Subtraktion zu bekommen

Verständnis dazu, welche Handlung hinter einer Operation steckt, Vorstellungen von einer Repräsentationsebene in einer andere übertragen. Beispielaufgaben (aus: Häsel-Weide et al 2017):

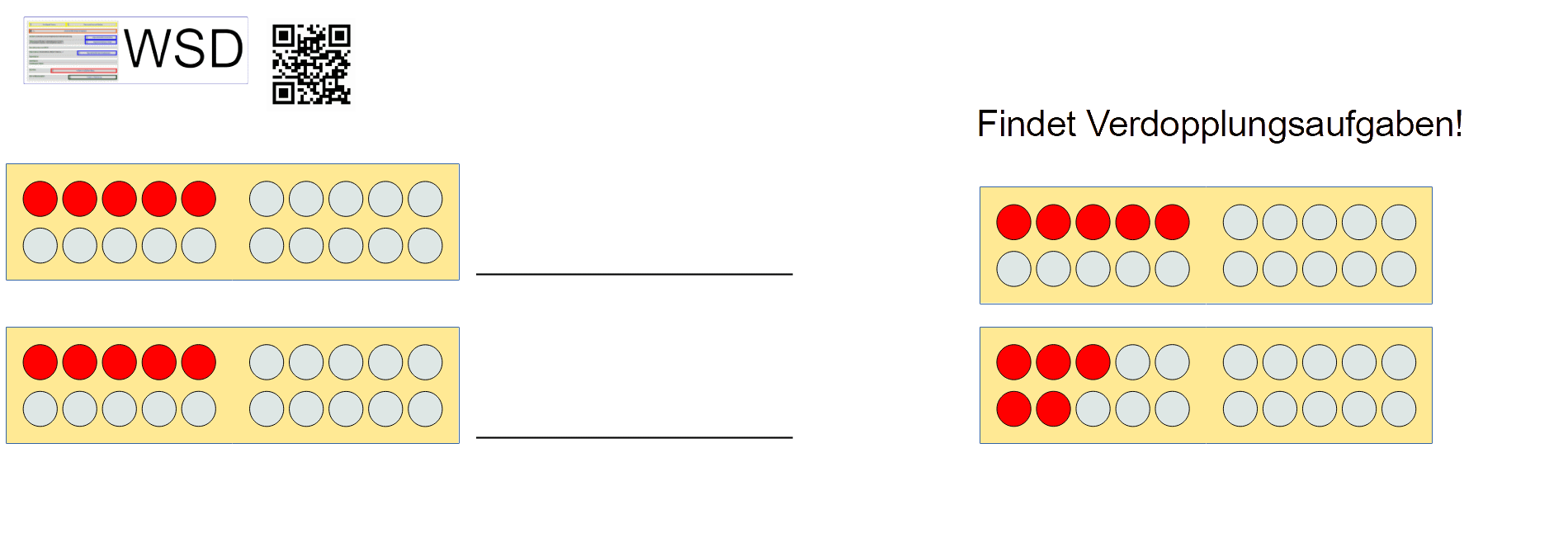
Zitiervorschlag: Grafik „Grundvorstellungen aufgreifen“ von Albrecht, C. (2022). Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:didaktisierung:nicht-zaehlende_strategie#grundvorstellungen_aufgreifen, CC BY-SA 4.0

Rechnen mit Zahlbeziehungen: Beziehungen zwischen Aufgaben erkennen und schwierige Aufgaben von einfachen abzuleiten lernen. Beispielaufgaben (aus: Häsel-Weide et al 2017):

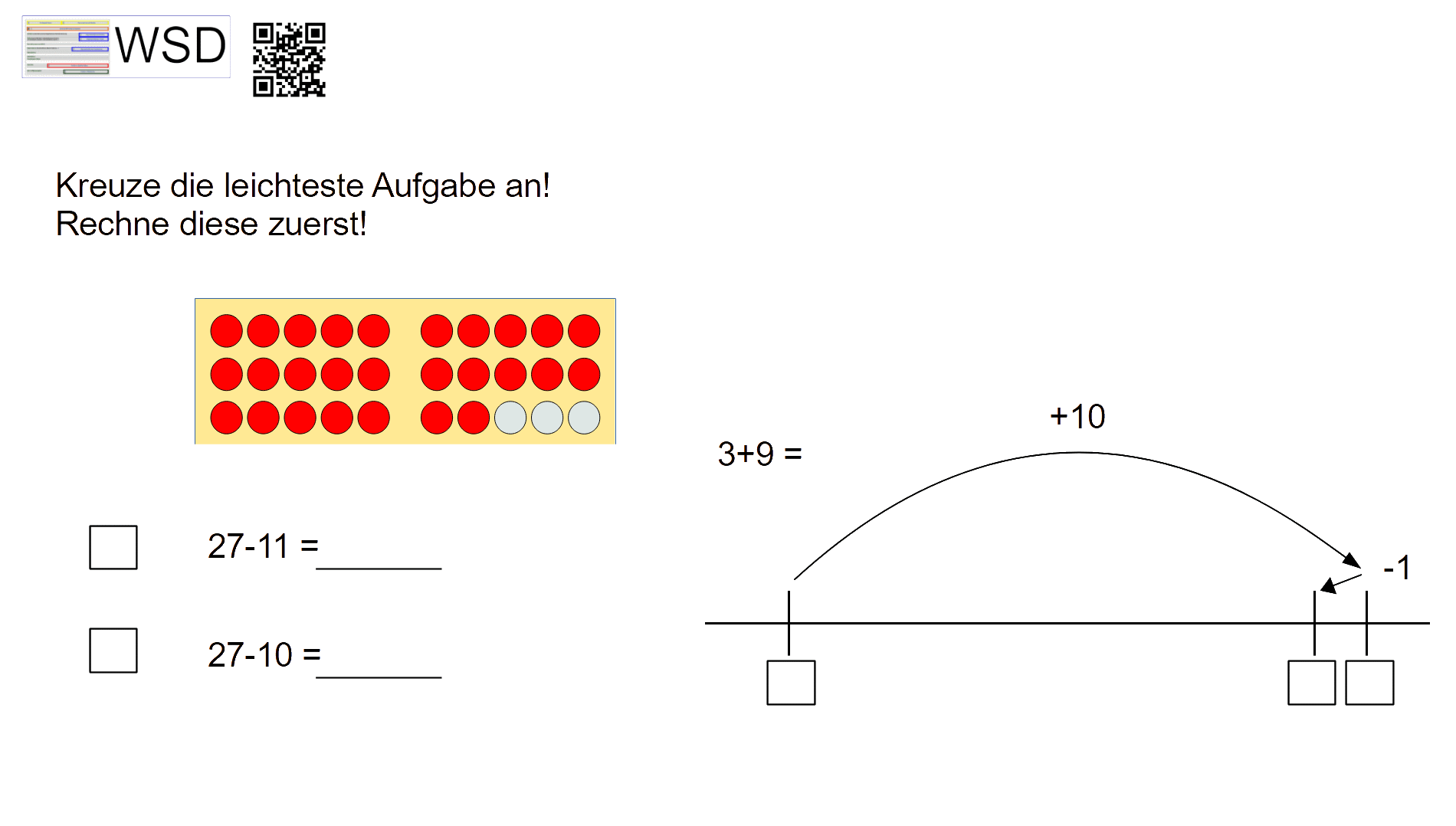
Zitiervorschlag: Grafik „Rechnungen mit Zahlbeziehungen“ von Albrecht, C. (2022). Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:didaktisierung:nicht-zaehlende_strategie#rechnungen_mit_zahlbeziehungen, CC BY-SA 4.0

Im Rahmen einer unterrichtsimmanenten Anregung zur Bevorzugung alternativer Strategien wird einerseits die Möglichkeit geboten, basale Kompetenzen aufzuarbeiten. Darüber hinaus werden den Kindern zahlreiche Möglichkeiten zur Strukturierung mathematischer Objekte über Operationen gegeben. Ziel ist hierbei, dass die Kinder den Vorteil operativer Strategien gegenüber dem scheinbar einfacheren Zählen erkennen (vgl. Häsel-Weide et al 2017). Eine Förderung, die hierbei aber auf das einzelne Kind ausgerichtet ist, isoliert den Lernprozess dieses Kindes von dem der anderen Kinder. Das Verstehen von Mathematik ist aber in besonderem Maße vom aktiven Erkennen mathematischer Zusammenhänge und der Ausdifferenzierung und Verallgemeinerung dieser durch interaktive Verständigungsprozesse abhängig (vgl. Häsel-Weide et al 2017). Kommunikative mathematische Begegnungen der Schüler:innen untereinander dürfen somit nicht vernachlässigt werden.

Das Prinzip der Parallelisierung (ursprünglich aus dem Bereich der Didaktik des jahrgangsgemischten Mathematikunterrichts) ermöglicht es hierbei, dass Schüler:innen auf unterschiedlichen Niveaus Erkenntnisse gewinnen und diese auch in der Klasse vorstellen können (vgl. Häsel-Weide et al 2017).

Primakom: Nicht-zählendes Rechnen

Häsel-Weide, U. & Nührenbörger, M. et al (2017). Ablösung vom zählenden Rechnen. Fördereinheiten für heterogene Lerngruppen. Seelze: Klett

Layout und Gestaltung: Christian Albrecht, Zentrum für Schulqualität und Lehrerbildung (ZSL) Baden-Württemberg