Inhaltsverzeichnis
Entdeckendes Lernen und produktives Üben im Mathematikunterricht
Zitiervorschlag: Marx, C. (2021). „Entdeckendes Lernen und produktives Üben“. Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:didaktisierung:entdeckendes_lernen_m, CC BY-SA 4.0
Ein wichtiges Ziel des Mathematikunterrichts ist es, dass Schüler:innen tragfähige Zahl- und Operationsvorstellungen entwickeln und somit (mathematische) Begriffe, Zusammenhänge und Verfahren sowie Vorgehensstrategien in variierenden Kontexten verfügbar haben. Dafür ist es unerlässlich, dass die Schüler:innen mathematische Strukturen und Sachverhalte im Rahmen sogenannter produktiver Übungsformen selbst aktiv entdecken und üben können.
Wissenschaftliche Erkenntnisse legen nahe, dass das Einführen und das Üben eines neuen Bildungsinhalts „eng miteinander verzahnt“ (Wittmann 1990) werden müssen. Indem beispielsweise von Beginn an durch gestützte Übungsphasen bereits Grundvorstellungen aufgebaut und Einsichten in Strukturen und Beziehungen gefördert werden, vertiefen und vernetzen die Schüler:innen ihr Vorwissen zum Thema und erweitern dabei systematisch dieses Wissen. Dies heißt also, dass Übungsphasen heute nicht mehr nur die reine Automatisierung eines Stoffes zum Ziel haben sollten, sondern dass Übungsprozesse die Ziele der Sicherung, Vernetzung und Vertiefung anstreben müssen, um das Wissen beweglich zu machen. Insgesamt kann in Anlehnung an Wittmann dann vom beziehungsreichen, produktiven Üben gesprochen werden, wenn die Schüler:innen zu selbstständigen Denkprozessen angeregt werden, sie bei Schwierigkeiten im aktiven Problemlösen unterstützt werden und die Aufgaben im Sinne einer natürlichen Differenzierung so aufgebaut sind, dass jedes Kind auf seinem Niveau mitarbeiten kann. Lehrpersonen müssen sich daher mit der Frage auseinandersetzen, wie produktive Übungsformate und Übungsphasen gestaltet werden können, in denen die Schüler:innen zum gleichzeitigen Entdecken und Üben bestimmter mathematischer Strukturen angeregt werden und so ein tieferes mathematisches Verständnis erlangen können.
Im produktiven Übungsprozess können je nach Grad der Strukturierung bzw. nach der Darstellungsform vier verschiedene Typen von Übungen unterschieden werden, die im Folgenden am Beispiel der Addition dargestellt werden.
Die vier Typen des produktiven Übens
Die folgende Tabelle illustriert zusammenfassend die vier Typen des produktiven Übungsprozesses. Darin wird deutlich, dass „das Üben Hand in Hand geht mit mathematischen Entdeckungen und Reflexionen“ (vgl. Leuders 2009). Zum anderen wird ersichtlich, dass produktives Üben als Prozess zu verstehen ist, in dem die Schüler:innen durch unterschiedlich strukturierte Aufgaben anhand gestützter und formaler Darstellungsformen sowohl Grundvorstellungen aufbauen, Beziehungen erkennen und vernetzen und diese Einsichten zunehmend automatisieren und schließlich als gesicherte Zahl- und Operationsvorstellungen flexibel zur Verfügung haben. Durch Phasen des Begründens und Argumentierens im gemeinsamen Gespräch werden hierbei automatisch auch prozessbezogene Kompetenzen erweitert. Als Faustregel hierbei gilt „so lange gestütztes Üben wie individuell nötig, so oft strukturiertes Üben wie möglich“.
Vier Typen des Produktiven Übens
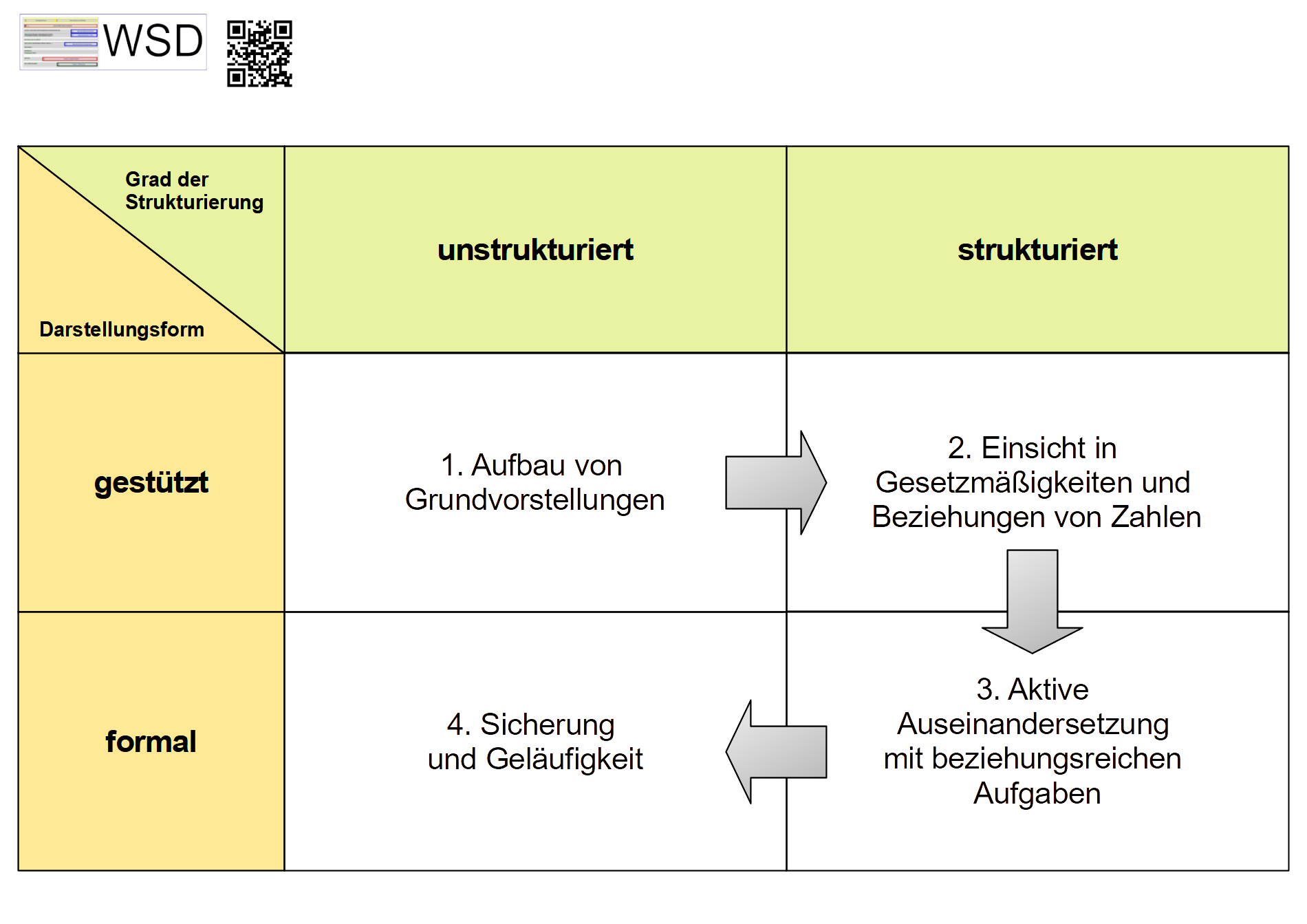
Zitiervorschlag: Grafik „Vier Typen des Produktiven Übens“ von Albrecht, C. (2022). Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:didaktisierung:entdeckendes_lernen_m#vier_typen_des_produktiven_übens, CC BY-SA 4.0
Aufbau von Grundvorstellungen
Ziel erster produktiver Übungsphasen ist es, zunächst durch das Anbieten unstrukturierter Materialien, Grundvorstellungen zur Addition anzubahnen. So erfahren die Schüler:innen das Prinzip des Addierens im Sinne eines Hinzufügens und erkennen, dass beim Addieren eine bestimmte Menge um eine oder mehrere Menge/n erweitert wird. In dieser gestützten Phase können beispielsweise konkretes Anschauungsmaterial wie Kastanien, Steine, Bauklötze, Geldscheine/Münzen oder ikonische Darstellungen genutzt werden. Ebenso können natürliche, konkrete Zählanlässe in der Klasse genutzt werden, um das additive Prinzip des Hinzufügens zu verdeutlichen (z.B. „Philipp wird heute acht Jahre alt, wie viele Kinder sind gleich alt/ älter/ jünger?“, „Du hast drei Punkte und bekommst noch zwei – wie viele hast du jetzt?“, „Ihr habt ein Tor geschossen, wie viele Tore habt ihr insgesamt?“).
Einsicht in Gesetzmäßigkeiten und Beziehungen von Zahlen
Im zweiten Schritt sollten die Schüler:innen anhand strukturierter, gestützter Übungen dazu angeregt werden, selbst Strukturen und Beziehungen zwischen den Zahlen und Aufgaben zu erkennen und diese Einsichten für den Lösungsprozess zu nutzen. Dies kann beispielsweise anhand von Übungsserien umgesetzt werden, die die Schüler:innen dazu auffordern die vorgegebenen Additionen mit Hilfe von Plättchen oder Rechenschiffen zunächst auszufüllen. Hierbei erkennen die Schüler:innen, dass die Menge fünf in unterschiedliche Teilmengen zerlegt werden kann und dass diese Teilmengen dabei unterschiedliche Mächtigkeiten annehmen können. Im nächsten Schritt sollen die Schüler:innen diese Entdeckungen an weiteren Summen durch das Finden der jeweiligen Summanden vertiefen. So wird anhand verschiedener gestützter und strukturierter Übungen beziehungsreiches Üben wie in folgender Abbildung dargestellt möglich.
Strukturierte und gestützte Übungen
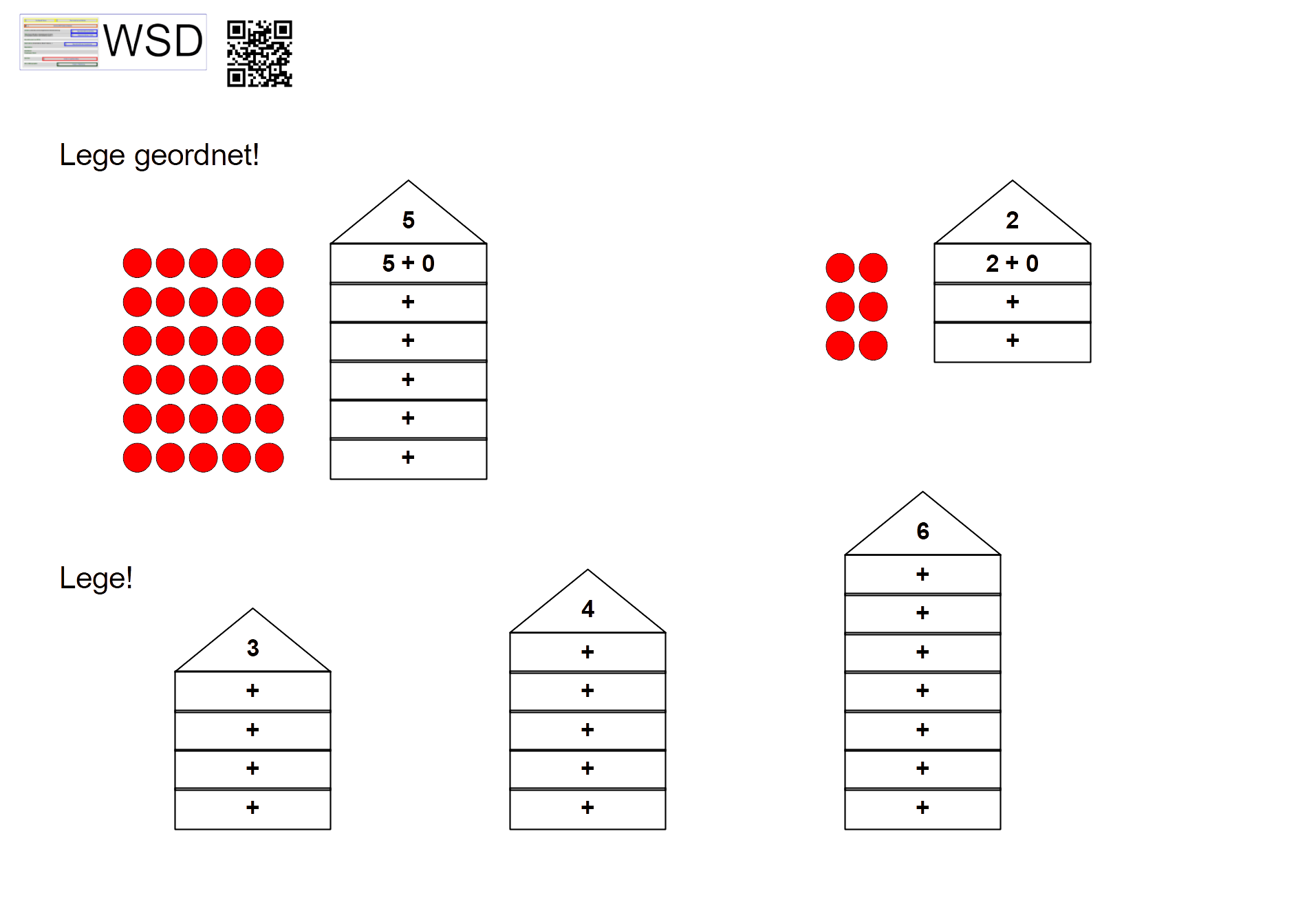
Zitiervorschlag: Grafik „Strukturierte und gestützte Übungen“ von Albrecht, C. (2022). Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:didaktisierung:entdeckendes_lernen_m#strukturierte_und_gestützte_übungen, CC BY-SA 4.0
Aktive Auseinandersetzung mit beziehungsreichen Aufgaben
Im dritten Schritt geht es darum, die gewonnen Einsichten anhand formaler werdender Übungsformate weiter zu vertiefen. Dies kann beispielsweise durch Übungsformate, wie in folgender Abbildung dargestellt, erfolgen. Hierbei müssen die Schüler:innen formal dargebotene Aufgabenpakete lösen, indem Beziehungen zwischen den einzelnen Aufgaben erkannt und zum Lösen der Aufgabe genutzt werden.
Formaler werdende Übungsformate

Zitiervorschlag: Grafik „Formaler werdende Übungsformate“ von Albrecht, C. (2022). Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:didaktisierung:entdeckendes_lernen_m#formaler_werdende_übungsformate, CC BY-SA 4.0
Sicherung und Geläufigkeit (Automatisierung)
Im vierten Schritt folgen vielfältige Übungsformen zum Automatisieren und zur Festigung des Gelernten. Zur Sicherung der Addition beispielsweise können hierfür formale, unstrukturierte Aufgaben, wie in folgender Abbildung dargestellt, verwendet werden. Ebenso können Aufgaben wie „Male die Felder je nach Ergebnis in der richtigen Farbe aus!“ in dieser Phase gezielt dazu verwendet werden, erarbeitetes Wissen zu Automatisieren. Formen der Automatisierung sollten allerdings nicht zu früh eingesetzt werden, sondern erst dann erfolgen, wenn die Schüler:innen tragfähige Vorstellungen in der geforderten Kompetenz entwickelt haben, denn „zu frühes oder reines Automatisieren führt meistens zu reinem Auswendiglernen“ (Wittmann & Müller 1992) und verhindert den Aufbau eines tieferen, vernetzten Verständnisses.
Automatisieren des Gelernten

Zitiervorschlag: Grafik „Automatisieren des Gelernten“ von Albrecht, C. (2022). Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:didaktisierung:entdeckendes_lernen_m#automatisieren_des_gelernten, CC BY-SA 4.0
Techniken für das Erzeugen produktiver Übungsaufgaben
In Anlehnung an Leuders (2009) liegt es in der Verantwortung der Lehrperson, produktive Übungsformate, die beziehungsreiches und vernetztes Üben und die Förderung von Einsichten in Aufgaben- und Zahlbeziehungen ermöglichen, zu erkennen, auszuwählen und bestehende Aufgaben zu modifizieren beziehungsweise selbst zu formulieren. Leuders beschreibt für das Erzeugen beziehungsweise das Modifizieren produktiver Übungsaufgaben verschiedene Kriterien, die im Folgenden knapp dargestellt werden.
| Form der Aufgabe/ Frage | Aufgabenbeispiele | |
|---|---|---|
| Umkehraufgabe | Wann kommt … heraus? | - Zahlenmauern |
| Funktionale Abhängigkeit | Was passiert, wenn …? | - Zahlenmauern („Was passiert, wenn man alle Basiszahlen um 1/2/3… erhöht?“) - Rechendreiecke („Was passiert, wenn man alle Außenzahlen um 1,2,3… erhöht?“) |
| Kombinatorische Abhängigkeit | Wie viele Möglichkeiten gibt es …? | - Rechenketten („Wie viele Möglichkeiten gibt es, die Zielzahl 5, 10, 20… zu erreichen?“) - Geldbeträge legen („Wie viele Möglichkeiten gibt es, insgesamt 5,10,20… Cent zu legen?“) - Schüttelboxen („Wie viele verschiedene Möglichkeiten findest du?“) - 10er/ 20er Rechenschiffe („Du hast 20 rote und 20 blaue Plättchen. Wie viele verschiedene Möglichkeiten findest du, das Rechenschiff ganz zu füllen?“) - Pentominos („Wie viele Formen kannst du mit diesen fünf Quadraten legen?“) |
| Eigene Aufgaben formulieren | Wie viele Aufgaben findest du…? | - „Wie viele verschiedene Aufgaben kannst du aus diesen vier Zahlen bilden?“ - Verliebte Zahlen („Wie viele verliebte Zahlen findest du zur Zahl 5?“) - Zahlenhäuser („Wie viele verschiedene Stockwerke findest du zum Zahlenhaus der 20?“) - Fingerbilder („Zeige mit jeweils beiden Händen insgesamt fünf Finger. Wie viele Aufgaben findest du?“) |
| Muster erkennen und fortführen | Wie lässt sich das Muster fortsetzen? | - Starke Päckchen („Wie könnten die nächsten Aufgaben heißen? - Schreibe auf!“) - Muster aus geometrischen Formen („Hier liegen zwei gelbe Rechtecke, ein grünes Quadrat - zwei Rechtecke, ein grünes Quadrat… Kannst du das Muster weiter legen?“) |
Die Anregungen in der Tabelle verdeutlichen, dass bestehende Aufgaben („Fülle die Zahlenmauer aus.“) schon durch eine leichte Modifizierung der Ausgangsfrage („Wie viele verschiedene Möglichkeiten findest du, diese Zahlenmauer auszufüllen?“) mit vergleichsweise wenig Aufwand so formuliert werden können, dass sie die Schüler:innen zu produktiven Übungsprozessen anregen. So wird es also möglich, dass die Schüler:innen in jeder Mathestunde neue Erfahrungen und Entdeckungen machen können. „Aktiv entdeckendes Lernen kann und muss also nicht nur in so genannten ‚Einführungsstunden‘ stattfinden, sondern auch in ‚Übungsstunden‘“ (Wittmann & Müller 1992).
Weiterführende Informationen
Literatur
Selter, C. & Zannetin, E. (2018). Mathematik unterrichten in der Grundschule, Klett.
Hacker, J.; Kuß, S. et al (2013). „Fördern inklusiv, Heft 4 – Zahlenraum bis 100“, Westermann.
Leuders, T. (2009). „Intelligent Üben und Mathematik erleben“, abgerufen von: https://home.ph-freiburg.de/leudersfr/preprint/2009_leuders_intelligent_ueben_mathemagische_momente.pdf
Wittmann, E. & Müller, G. (1990). „Handbuch produktiver Rechenübungen“, Klett.
Layout und Gestaltung: Christian Albrecht, Zentrum für Schulqualität und Lehrerbildung (ZSL) Baden-Württemberg