Inhaltsverzeichnis
Darstellungsmittel einsetzen
Zitiervorschlag: Marx, C. (2021). „Darstellungsmittel einsetzen“. Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:didaktisierung:darstellungsmittel_m, CC BY-SA 4.0
Ein Ziel des Mathematikunterrichts ist es, bei den Schüler:innen tragfähige Zahl- und Operationsvorstellungen zu entwickeln, sodass ein sicheres und flexibles Rechnen ohne Hilfsmittel möglich wird.
Um dieses Ziel zu erreichen, ist es wichtig sich zu verdeutlichen, wie mentale Repräsentationen bzw. mathematische Vorstellungsbilder in den Köpfen der Kinder entstehen. In Anlehnung an Wartha & Schulz et al (2012) entwickeln Kinder abstraktes mathematisches Denken ausgehend von konkreten Handlungen über Bilder und mental vorgestellte Rechenwege. Diese mathematische Begriffsbildung sollte durch den gezielten Einsatz verschiedener Darstellungsformen und Darstellungsmittel individuell unterstützt werden, da diese zur Veranschaulichung mathematischer Strukturen dienen. Richtig eingesetzt helfen Darstellungsformen und Darstellungsmittel schließlich dabei, Zahl- und Operationsvorstellungen aufzubauen sowie Rechenwege nachvollziehbar darzustellen.
Um im Unterricht Darstellungsformen passgenau auswählen zu können, muss man sich zunächst mit möglichen Darstellungsmitteln, deren Formen und Einsatz auseinandersetzen. Der Begriff Darstellungsformen beschreibt hierbei die vier Dimensionen Handlung, Sprache, Bild und Symbol, in denen Zahlen und Mengen dargestellt werden können und die das Kind dabei unterstützen, allmählich mentale Repräsentationen zu entwickeln. Beim Einsatz dieser vier Darstellungsformen kann man schließlich jeweils auf verschiedene Darstellungsmittel zurückgreifen, um Zahlen und Mengen zu repräsentieren. Möchte man beispielsweise die Menge fünf über die Darstellungsform der Handlung mit den Kindern erarbeiten, kann die Lehrperson entweder auf strukturierte (Würfelbild der fünf) oder unstrukturierte Darstellungsmittel (fünf Kastanien) zurückgreifen. Unterschiedliche Darstellungsmittel helfen also dabei z.B. Anzahlen, Operationen oder Rechenwege auf der jeweiligen Darstellungsform zu verdeutlichen und sie unterstützen die einzelnen Entwicklungsschritte ausgehend von konkreten Handlungen bis zur mentalen Repräsentation.
Darstellungsformen und deren Darstellungsmittel
Die vier Darstellungsformen Handlung – Sprache – Bild – Symbol und deren Darstellungsmittel werden im Folgenden tabellarisch dargestellt. Insgesamt sollten Materialien letztendlich immer kritisch gesichtet, auf ihre jeweiligen Vor- und Nachteile hin überprüft und evtl. mit den Kindern gemeinsam nach dem Motto so viel wie nötig und so passend wie möglich ausgewählt und anschließend reflektiert eingeführt werden.
| Darstellungsmittel | ||
|---|---|---|
| Darstellungsform | Spektrum | Einsatz |
| Handlung | unstrukturiert - Naturmaterialien (Steine, kastanien, Nüsse…) - Alltagsmaterialien (Wäscheklammern, Spielfiguren, Bauklötze…) - didaktisches Material (Ziffernkarten, Wendplättchen…) - didaktische Materialien (Zahlenbilder, Rechenketten, Rechenrahmen, 10er-System-Material, 20er/100er-Feld, Finger…) | - aktives, passives, spielerisches Handeln - Handeln zu Rechengeschichten, Bildergeschichten, Termen, Gleichungen |
| Sprache | mündlich - zuhören - sprechen - erklären - nachfragen - begründen - schriftlich - abschreiben/abzeichnen - aufschreiben | - Gedanken kommunizieren untereinander (Partner:innen-/Gruppengespräch, Plenum, Mathekonferenz) - Selbstreflexion über Rechenwege, Selbsteinschätzungsbögen - Mathematische Sachverhalte ausdrücken, z.B. in Rechengeschichten, Beschreibungen, Erklärungen, Beweise |
| Bild | Bilder von alltäglichen Symbolen - Zeichnungen - Skizzen Bilder von didaktischem Material - Mengenbilder - Strichlisten - Punktebilder | - zeichnen und deuten - Handlungen, Rechengeschichten, Mengen darstellen und Terme daraus ablesen |
| Symbol | mathematische Symbole - Zahlen - Terme - Gleichungen - Zahlenmauern | - Rechengeschichten, Bilder, Handlungen in mathematische Symbole bzw. formale Zahlen übersetzen |
Beziehungen der Darstellungsformen
Die folgende beispielhafte Darstellung unterstreicht, dass die beschriebenen Darstellungsformen nicht chronologisch oder linear zueinander in Beziehung stehen, sondern dass sich diese aufeinander beziehen und gegenseitig ergänzen. Somit darf auch der Einsatz verschiedener Darstellungsformen im Unterricht nicht linear bzw. chronologisch erfolgen, sondern flexibel, sich ergänzend und im Wechsel zueinander:
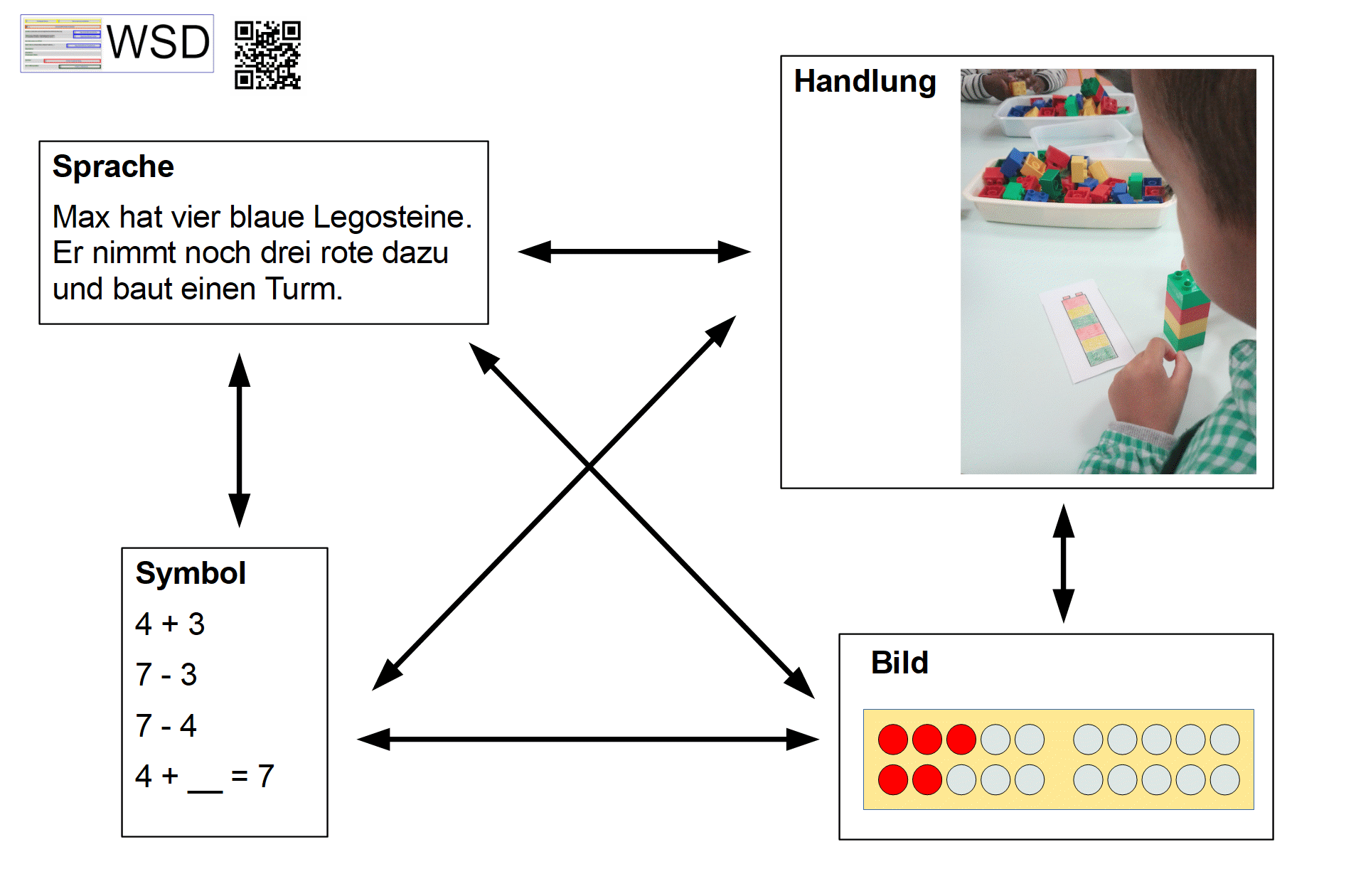
Zitiervorschlag: Grafik „Beziehungen der Darstellungsformen“ von Albrecht, C. (2022). Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:didaktisierung:darstellungsmittel_m#beziehungen_der_darstellungsformen, CC BY-SA 4.0
Auswahl passgenauer Darstellungsmittel
Das Spektrum der Darstellungsformen lässt die Vielzahl an möglichen Materialien erahnen. Da allerdings nicht alle Materialien gleichermaßen für alle Kinder und alle Themen geeignet sind, werden nachfolgend in Anlehnung an Pikas vier Kriterien zur Auswahl didaktischer Materialien skizziert:
Qualität vor Quantität
Das Darstellungsmittel allein muss zunächst als Lerngegenstand betrachtet werden, denn es ist nicht selbsterklärend. D.h. das Kind muss durch die konkrete Handlung mit dem jeweiligen Material dessen Struktur durchdringen und den dahinter liegenden abstrakt mathematischen Begriff verstehen, um überhaupt produktiv mit diesem Material arbeiten zu können. Dann erst können mathematische Strukturen und Muster erkannt, zueinander in Beziehung gesetzt und mentale Vorstellungsbilder generiert werden. Werden beispielsweise zu viele Materialien nebeneinander dargeboten, wird dieses Durchdringen deutlich schwerer. In Anlehnung an Wittmann gilt daher bei der Auswahl die Prämisse „Weniger ist mehr!“ (Wittmann 1993 in Pikas), denn nachhaltiger Lernerfolg steigt „nicht mit der Masse der Materialien, sondern mit der Reichhaltigkeit und Intensität der Schüler:innenaktivitäten“ (Müller/ Wittmann in Pikas). Dass Darstellungsmittel weder selbsterklärend noch von allen Kindern gleich interpretiert werden, zeigt die folgende Abbildung, in der rechts verschiedene Interpretationen zu den links stehenden Bildern aufgeführt sind:
Interpretationen verschiedener Darstellungsmittel
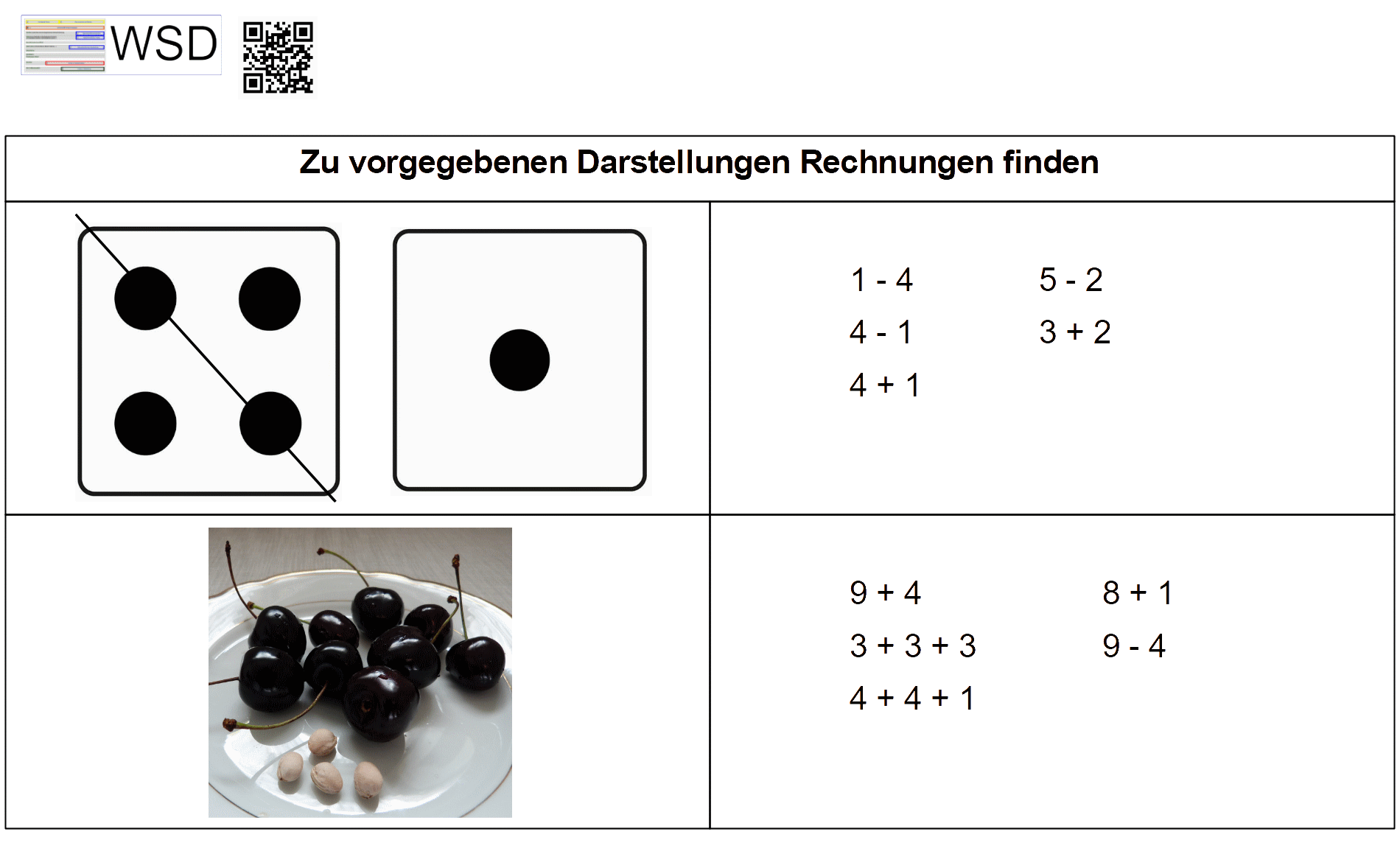
Zitiervorschlag: Grafik „Interpretationen verschiedener Darstellungsmittel“ von Albrecht, C. (2022). Abgerufen von URL: https://wsd-bw.de/doku.php?id=wsd:didaktisierung:darstellungsmittel_m#interpretationen_verschiedener_darstellungsmittel, CC BY-SA 4.0
Kritische Reflexion der Vor- und Nachteile
Das Spektrum der Darstellungsformen verdeutlicht nicht nur die Vielfalt der Auswahlmöglichkeiten, sondern zeigt auch, wie unterschiedlich Materialien aufgebaut sind (z.B. strukturiert vs. unstrukturiert, Alltagsmaterial vs. didaktisches Material usw.). Daraus folgt, dass nicht jedes Material alles kann bzw. dass Materialien je nach Thema, Ziel und Zahlenraum Vorteile bzw. Nachteile haben können. Lehrpersonen sollten sich daher bei jedem Material verschiedene Fragen stellen, wie beispielsweise (vgl. Pikas):
| Praktische Fragen | - Ist das Material leicht handhabbar, haltbar, seinen Preis wert? - Passt dieses Material zu diesem Thema? - Passt das Material für die Schüler/ einzelne Schüler |
|---|---|
| Didaktische Fragen | - Können Mengen simultan/ quasi-simultan erfasst werden? Wird die dezimale Struktur sichtbar/ erfahrbar? - Können Zusammenhänge zwischen den verschiedenen Darstellungsformen hergestellt werden? - Werden ordinale und kardinale Zahlaspekte deutlich? - Können verschiedene Aufgaben dargestellt werden? |
Die folgende Tabelle zeigt exemplarisch für das Thema „Rechenwege darstellen“ eine solche pro-contra Überlegung:
| Welche Darstellungsmittel eignen sich, um Rechenwege anschaulich darzustellen? | ||
|---|---|---|
| Darstellungsmittel | Pro | Contra |
| Finger | - Erste natürliche Zählstrategien (vorwärts, rückwärts, in Schritten…) sind mit den Fingern darstellbar bzw. werden häufig oft automatisch als Hilfsmittel verwendet - Strukturiertes Zählen kann angebahnt werden - Simultane und quasi-simultane Anzahlauffassung kann geschickt geübt werden - Unterschied zwischen Kardinalzahl- und Ordinalzahlaspekt wird deutlich (drei Finger vs. der 3. Finger) - Grundlegende Einsicht in Fünfer- und Zehnerstruktur wird möglich, Kraft der fünf wird deutlich - Vorgänge des Hinzufügens und Wegnehmens im Zahlenraum bis 10 anschaulich darstellbar - Teil-Ganzes Beziehungen im Zahlenraum bis zehn sind schnell darstellbar - sind immer kostengünstig „griffbereit“ | - verleiten zum zählenden Rechnen - Kinder brauchen gezielte Unterstützung bei der Entwicklung vom zählenden zum nicht-zählenden Verwenden der Finger - im Zahlenraum >10 wird das Rechnen mit Fingern ungeschickter, da die Kinder sich merken müssen, wie oft die Hände „durchgezählt“ wurden |
| Rechenrahmen/ Rechenschiff | - Unterschied zwischen Kardinalzahl- und Ordinalzahlaspekt wird deutlich (drei rote Plättchen vs. das 3. rote Plättchen) - Schrittweiser Zehnerübergang handelnd darstellbar - Grundlegende Einsicht in Fünfer- und Zehnerstruktur wird möglich, Kraft der fünf wird deutlich - Strukturierte Anzahlerfassungen sind gut umsetzbar auf verschiedenen Wegen (Verdopplungen, Addition über den Zehner im Teilschrittverfahren) - Entlastet Kurzzeitgedächtnis, da Rechenschritte beim Zehnerübergang sichtbar sind und das Kind sich diese nicht merken muss, so werden Gedächtniskapazitäten frei und das Kind kann Strukturen erfassen | - verleitet zum zählenden Rechnen - Kinder brauchen gezielte Unterstützung bei der Ablösung von einer zählenden zu einer strukturierten Anzahlerfassung |
| Cuisenaire Stäbe | - Kardinalzahlaspekt wird deutlich, da die einzelnen Stäbe jeweils eine Menge darstellen - Teil-Ganzes-Konzept von Anzahlen gut darstellbar, da Mengen in verschiedenen Teilmengen dargestellt werden können - Rechenoperationen lassen sich verdeutlichen - Prozesse des Bündelns und Entbündelns sind handelnd darstellbar, so kann Entwicklung des Stellenwertverständnisses unterstützt werden - Erweiterung des Materials in höhere Zahlenräume mit Cuipsi Platten und Cuipsi Quadern | - Einheiten der einzelnen Stäbe müssen gesichert sein, sonst sind Fehlinterpratationen möglich (wenn das Kind z.B. den blauen Stab mental mit der Menge zehn verbindet, kann das Kind die fehlerhafte Interpretation „10 ist um 1 größer als 8“ entstehen) - Bündelung und Entbündelung muss gesichert sein - Gefahr, dass Kind zur Unterscheidung seine Aufmerksamkeit auf die verschiedenen Farben legt anstatt auf die Länge der Stäbe („die 1 ist immer weiß“ oder „blau ist immer 9“) - Stäbe sind nicht teilbar und somit sind Muster nur nebeneinander vergleichbar und nicht veränderbar |
| 100er Tafel/ 1000er Buch | - Zahlbeziehungen werden deutlicher - Addition/ Subtraktion voller Zehner/ Hunderter geschickt darstellbar | - mentale Vorstellung über den 100er/1000er Raum muss entwickelt sein, um Zahlbeziehungen erkennen zu können - verleitet zum zählenden Rechnen - Zahlbeziehungen nicht immer deutlich zu erkennen, da z.B. die Zahl 21 weiter weg ist von der 20 als die 30 |
| 10er System Material (Dienes) | - Schrittweises Rechnen über Handlung umsetzbar, so dass Prinzip des Dazutuns/ Wegnehmens erfahrbar wird - Prozesse des Bündelns und Entbündelns sind handelnd darstellbar, so kann Entwicklung des Stellenwertverständnisses unterstützt werden | - Einheiten müssen klar sein, sonst sind Fehlinterpretationen möglich (z.B. bei der Darstellung der Rechnung 7+5 liegen eine Zehnerstange und zwei Einer Würfel, die vom Kind als Ergebnis „3“ gedeutet werden könnten - Bündelung und Entbündelung muss gesichert sein |
| Zahlenstrahl/ Rechenstrich | - Verdeutlicht Ordinalzahlaspekt, da die Ziffern in ihren Positionen in der Zahlenreihe erkennbar werden - Verbindung zwischen Ordinal- und Kardinalzahlaspekt kann hergestellt werden, indem Fokus von der Zahlenreihe mit ihren einzelnen Ziffern auf die gesamte zurückgelegte Strecke bis zu einer bestimmten Ziffer betrachtet wird - Bietet Gesprächsanlass über verschiedene Rechenwege - Umkehroptionen und Rechenstrategien gut darstellbar | - verleitet zum zählenden Rechnen - Lässt daher keine Entwicklung von Rechenstrategien zu, sondern setzt das Vorhandensein einer mentalen Rechenstrategie voraus |
Frage der Erweiterbarkeit in höhere Zahlenräume
Da Aufbau, Struktur und Einsatz der Darstellungsmittel per se immer von den Kindern zunächst durchdrungen werden müssen, ist es sinnvoll, von Anfang an Material auszuwählen und einzuführen, das in den folgenden Schuljahren und höheren Zahlenräumen weiterhin genutzt werden kann. Hierzu gehören z.B. das Material aus dem Programm mathe 2000 (Plättchen, Zwanzigerfeld, Hunderterfeld, Tausenderbuch..) oder das 10-er System-Material nach Dienes.
Abgleich mit dem eigenen Lehrwerk
Jedes Lehrwerk nutzt unterschiedliche Darstellungsmittel und -formen. Setzt man im Unterricht aus Gründen der Verfügbarkeit an der Schule beispielsweise Holzwürfel statt Wendeplättchen ein, muss dieser Darstellungswechsel den Kindern transparent gemacht und erklärt werden.
Aufbau mentaler Repräsentationen im Unterricht und die Gestaltung von Ablöseprozessen
Hat man sich als Lehrperson mit der Vielzahl zur Verfügung stehender Darstellungsmittel auseinander gesetzt und diese anhand der oben beschriebenen Kriterien ausgewählt und reflektiert, geht es darum, das Darstellungsmittel im Unterricht so einzusetzen, dass sich tragfähige, mentale Repräsentationen entwickeln können. Wie eingangs beschrieben, findet diese Entwicklung ausgehend von konkreten Handlungen über bildliche Darstellungen bis hin zu mentalen Bildern im Kopf statt. In Anlehnung an Wartha/ Schulz (2012) kann diese Entwicklung „vom konkreten Handeln zum Operieren in der Vorstellung“ durch den gezielten Einsatz von Darstellungsmitteln in den folgenden vier Phasen unterstützt werden:
Konkrete Phase 1: Kind handelt am geeigneten Material
- Kind handelt am geeignetem Material und verbalisiert Handlung bzw. mathematische Symbole
- Beispiel: „Ich nehme erst sechs Steine, dann noch vier bis zur Zehn, dann die restlichen drei, also 13.“
Konkrete Phase 2: Kind beschreibt die Materialhandlung mit Sicht auf das Material
- Kind diktiert einem Partner die Handlung, beobachtet die Handlung des Partners und kontrolliert den Handlungsprozess
- Beispiel: „Du nimmst erst sechs Steine, dann noch vier bis zur Zehn, dann die restlichen drei, also 13.“
Auf den Weg in den Kopf: Kind beschreibt die Materialhandlung ohne Sicht auf das Material
- Kind muss sich die Handlung im Kopf vorstellen und beschreiben während ein Partner die Handlung durchführt
- Beispiel: „Du nimmst erst sechs Steine, dann noch vier bis zur Zehn, dann die restlichen drei, also 13.“
Mentales Agieren: Kind beschreibt die Materialhandlung „nur“ in der Vorstellung
- Richtig rechnen im Kopf
- Beispiel: „Ich nehme erst sechs Steine, dann noch vier bis zur Zehn, dann die restlichen drei, also 13.“
Hierbei muss betont werden, dass der Darstellungswechsel Handlung – Bild – mentale Ebene nicht zu schnell erfolgen darf. Eine verfrühte Ablösung von enaktiven oder bildlichen Darstellungsformen birgt die Gefahr, dass das Kind noch keine (mentale) Einsicht in das dezimale Bündelungs- und Stellenwertprinzip erreicht hat und somit keine flexiblen Zählstrategien entwickeln konnte.
Verfestigtes zählendes Rechnen, wahlloses Hantieren mit Stellenwerten und eine unzureichende Zahl- und Operationsvorstellung können die Folge sein.
Um herauszufinden, wie weit das Kind jeweils in seinen mentalen Repräsentationen entwickelt ist, sind Gespräche über Lösungswege, Gedanken und Ideen als grundlegende diagnostische Prozesse zentral. Kommunikationssituationen sind also letztendlich der Schlüssel auf dem Weg zum Rechnen ohne Darstellungsmittel. Sie regen die Kinder zum weiteren entdecken, beschreiben und begründen an und geben somit der Lehrperson auch die Möglichkeit zu erkennen, ob das Kind das Darstellungsmittel noch benötigt oder nicht. Grundlegend hierbei ist, dass ein und dasselbe Kind dabei für unterschiedliche Themen und für unterschiedliches Material auf verschiedenen Entwicklungsstufen stehen kann und dass daher Ablöseprozesse langsam und im engen Austausch mit dem Kind erfolgen sollten.
Kann ein:e Schüler:in sicher mit verschiedenen Darstellungsformen umgehen und flexibel zwischen diesen wechseln, so hat die:derjenige ein sicheres, mentales Verständnis dieses Themas erlangt. Dann können Ablöseprozesse eingeleitet werden, indem seltener auf Darstellungsmittel zurückgegriffen wird und die Kinder dazu ermutigt werden, sich ohne Hilfsmittel an das Lösen von Aufgaben zu machen.
Weiterführende Informationen
Literatur
Selter, C. & Zannetin, E. (2018). Mathematik unterrichten in der Grundschule, Klett.
Gaidoschik, M. (2012), Viele Wege führen über den Zehner, abgerufen von: http://www.recheninstitut.at/wp-content/uploads/2012/04/Zehner%C3%BCbergang.pdf
Mix, U. (2018). Rechnen lernen mit Fingern?, abgerufen von: https://www.deutschlandfunk.de/labor-mathematik-unterricht-rechnen-lernen-mit-fingern.680.de.html?dram:article_id=416728.
Wartha, S. & Schulz, A. et al (2012). Rechenproblemen vorbeugen, Lehrerbücherei Grundschule.
Timmerevers, A. & Linnemann, U. (2011). Kopf und Zahl, abgerufen von https://www.rechenschwaeche.de/Kopf_und_Zahl/Kopf_und_Zahl_15.pdf.
Layout und Gestaltung: Christian Albrecht, Zentrum für Schulqualität und Lehrerbildung (ZSL) Baden-Württemberg